Angle Theorem Interior Sum

Interior angle = sum of the interior angles of a polygon / n. where “n” is the number of. This theorem states that the sum of the measures of the interior angles of a convex polygon with n sides.

Theorem 39: if a convex polygon has n sides, then its interior angle sum is given by the following equation: s = ( n −2) × 180°. the polygon in figure 1 has seven sides, so using theorem 39 gives: an exterior angle of a polygon is formed by extending only one of its sides. the nonstraight angle adjacent to an interior angle is the exterior angle. Oct 15, 2013 learn about the interior and the exterior angles of a polygon. a polygon is a plane shape bounded by a finite chain of straight lines. the interior . Exterior angle theorem. the measure of an exterior angle (our w) of a triangle equals to the sum of the measures of the two remote interior angles (our x and y) of the triangle. let's try two example problems. example a: if the measure of the exterior angle is (3x 10) degrees, and the measure of the two remote interior angles are 25 degrees.

Description the angle sum theorem. after this lesson, you will be able to prove that the interior angles in a triangle always angle theorem interior sum sum to 180˚. the lesson begins by .

Inscribed Angle Wikipedia

An interior angle is an angle inside a shape. example: pentagon. a pentagon has 5 sides, and can be made from three triangles, so you know what.. its interior angles add up to 3 × 180° = 540° and when it is regular (all angles the same), then each angle is 540° / 5 = 108° (exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up. The sum of its interior angles is 360 degrees. we can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. in the image given below, a trapezoid (also a type of quadrilateral) is shown. The sum of interior angles is 180 degrees (triangle angle sum theorem). all interior angles of a triangle are more than 0° but less than 180°. the bisectors of all the three interior angles intersect inside a triangle at a point called the in-center, which is the center of the in-circle of the triangle. In order to find the measure of a single interior angle of a regular polygon (a polygon with.

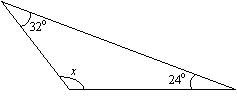
The triangle sum theorem states that the sum of the three interior angles in a triangle is always 180°. the triangle sum theorem is also called the triangle angle sum theorem or angle sum theorem. example: find the value of x in the following triangle. solution: x + 24° + 32° = 180° (sum of angles is 180°) x + 56° = 180°. Sum of interior angles of a polygon. we first start with a triangle (which is a polygon with the fewest number of sides). we know that. the sum of interior angles in a triangle is 180°. this is also called the triangle sum theorem. click here if you need a proof of the triangle sum theorem. Or, the sum of angles of a quadrilateral is 360°. this is the angle sum property of quadrilaterals. quadrilateral angles. a quadrilateral has 4 angles. the sum of its interior angles is 360 degrees. we can find the angles of a quadrilateral if we know 3 angles or 2 angles or 1 angle and 4 lengths of the quadrilateral. (n-2)x 180 degrees : the formula for finding the sum of all angles in a polygon ( regular). here "n" represents the number of sides of the polygon. for example  .

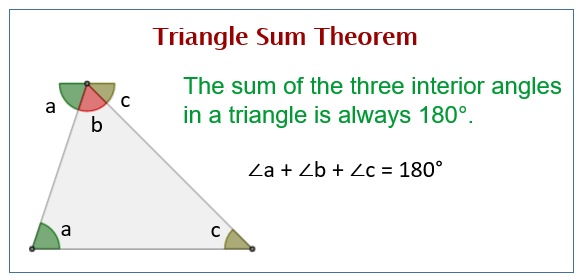
Angle Sum Theorem Basic Mathematics

Angle sum theorem: the angle measures in any triangles add angle theorem interior sum up to 180 degrees. key concept : alternate interior angles are equal. we will accept this fact without a proof. Rule 2: sides of triangle -triangle inequality theorem : this theorem states that the sum of the lengths of any 2 sides of a triangle must be greater than the third side. rule 3: relationship between measurement of the sides and angles in a triangle: the largest interior angle and side are opposite each other. Because the interior angles always add to 180°, every angle must be less than 180° the bisectors of the three interior angles meet at a point, called the incenter, which is the center of the incircle of the triangle. note the interior angles only add to 180° when the triangle is planar, meaning it is lying on a flat plane. if the triangle is. A special case of the theorem is thales' theorem, which states that the angle subtended by a diameter is always 90°, i. e. a right angle. as a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle.

Learn the formal proof that shows the measures of interior angles of a triangle sum to 180°. theorems concerning triangle properties. properties of . Angle sum property of a triangle & exterior angle theorem a triangle is the smallest polygon which has three sides and three interior angles. in this article, we are going to discuss the angle sum property and the exterior angle theorem of a triangle with its statement and proof in detail.

Theorem: the sum of the measures of the interior angles of a triangle is 180°. given: Δxyz. prove: m . In geometry, an inscribed angle is the angle formed in the interior of a circle when two secant lines intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.. the inscribed angle theorem relates the measure of an inscribed angle. See more videos for interior angle sum theorem. Jul 18, 2012 the triangle sum theorem states that the interior angles of a triangle add up to \ begin{align*}180^\circ\end{align*}. the above investigation is .

Exterior Angle Theorem Wikipedia

Angle Sum Of Polygons Cliffsnotes

Polygon interior angles sum theorem varsity tutors.

Triangle sum theorem explanation & examples.

Sum of angle theorem interior sum interior angles = 1,800 ° now, let's find one interior angle (n 2) × 180 ° n (12 2) × 180 ° 12. 10 × 180 ° 12. 1,800 ° 12. one interior angle = 150 ° awesome! sum of exterior angles. every regular polygon has exterior angles. these are not the reflex angle (greater than 180 °) created by rotating from the exterior of one. Triangle angle sum. in any triangle, there are always three interior angles. these inside angles always add up to 180°. this rule is very helpful in finding missing angles in a triangle. exterior angle theorem isosceles and equilateral triangles proving triangles congruent triangle angle sum triangles and congruence constructions. An interior angle is an angle inside a shape. example: the interior angles of a triangle add up to 180°. let's try a sum of interior angles = (n−2) × 180°.

In several high school treatments of geometry, the term "exterior angle theorem" has been applied to a different result, namely the portion of proposition 1. 32 which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. this result, which depends upon euclid's parallel. About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators.